Introduction to NumPy

MScAS 2025 - DSAS Lecture 2

Ilia Azizi

2025-09-30

Why NumPy?

Core Benefits

  • Efficient storage of numerical arrays (10–100× faster than Python lists)
  • Vectorized operations eliminate slow Python loops
  • Foundation for the Python data ecosystem (pandas, scikit-learn, etc.)
  • Broadcasting enables operations on arrays of different sizes

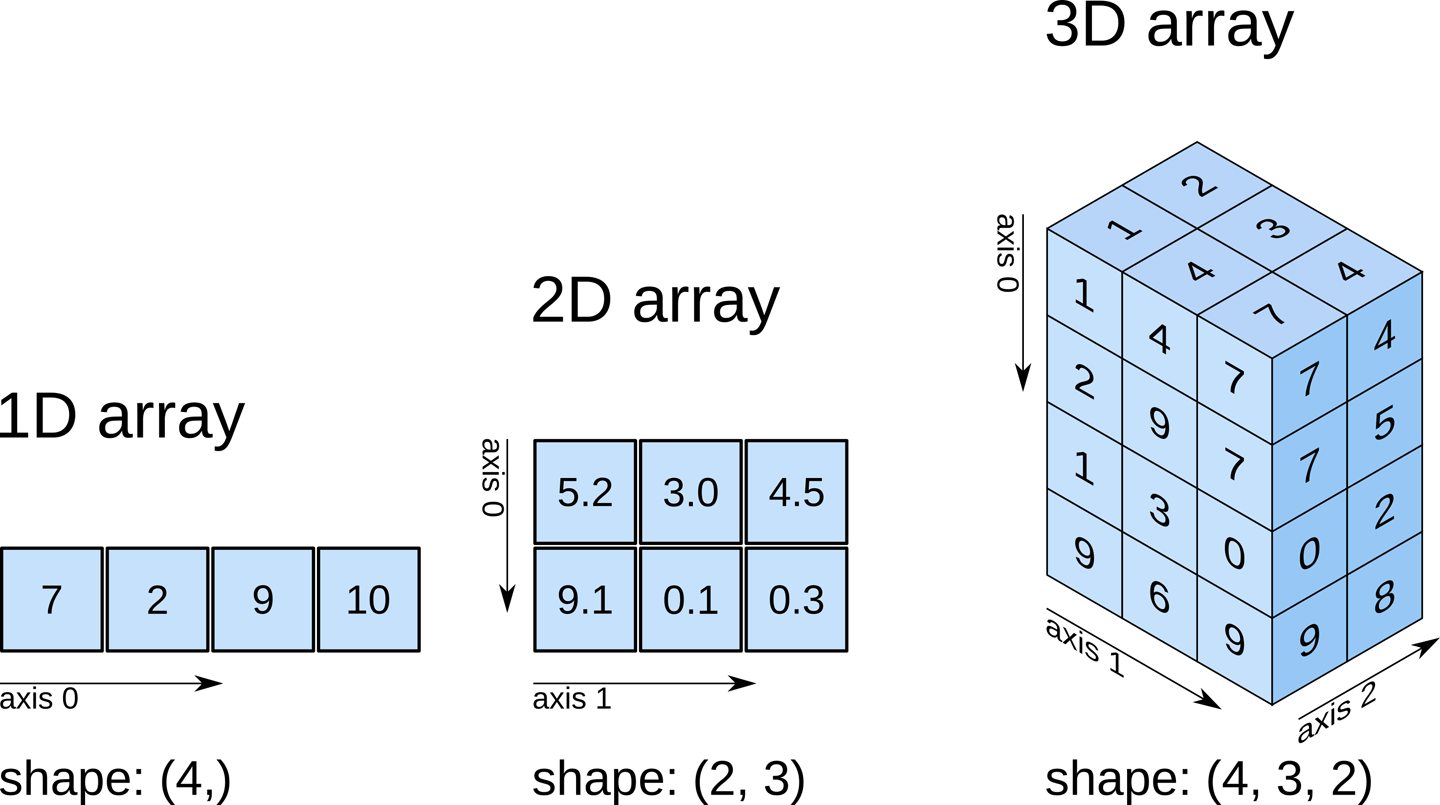
Array Basics

Note

Unlike Python lists, arrays contain elements of the same data type.

arange vs linspace

  • np.arange(start, stop, step): Creates values with fixed step size
    • Example: arange(0, 20, 5) → [0, 5, 10, 15] (stops before 20)
    • Like Python’s range(), endpoint is excluded
  • np.linspace(start, stop, num): Creates num evenly spaced values
    • Example: linspace(0, 10, 5) → [0.0, 2.5, 5.0, 7.5, 10.0] (includes 10)
    • Endpoint is included by default
    • Use when you need a specific number of points

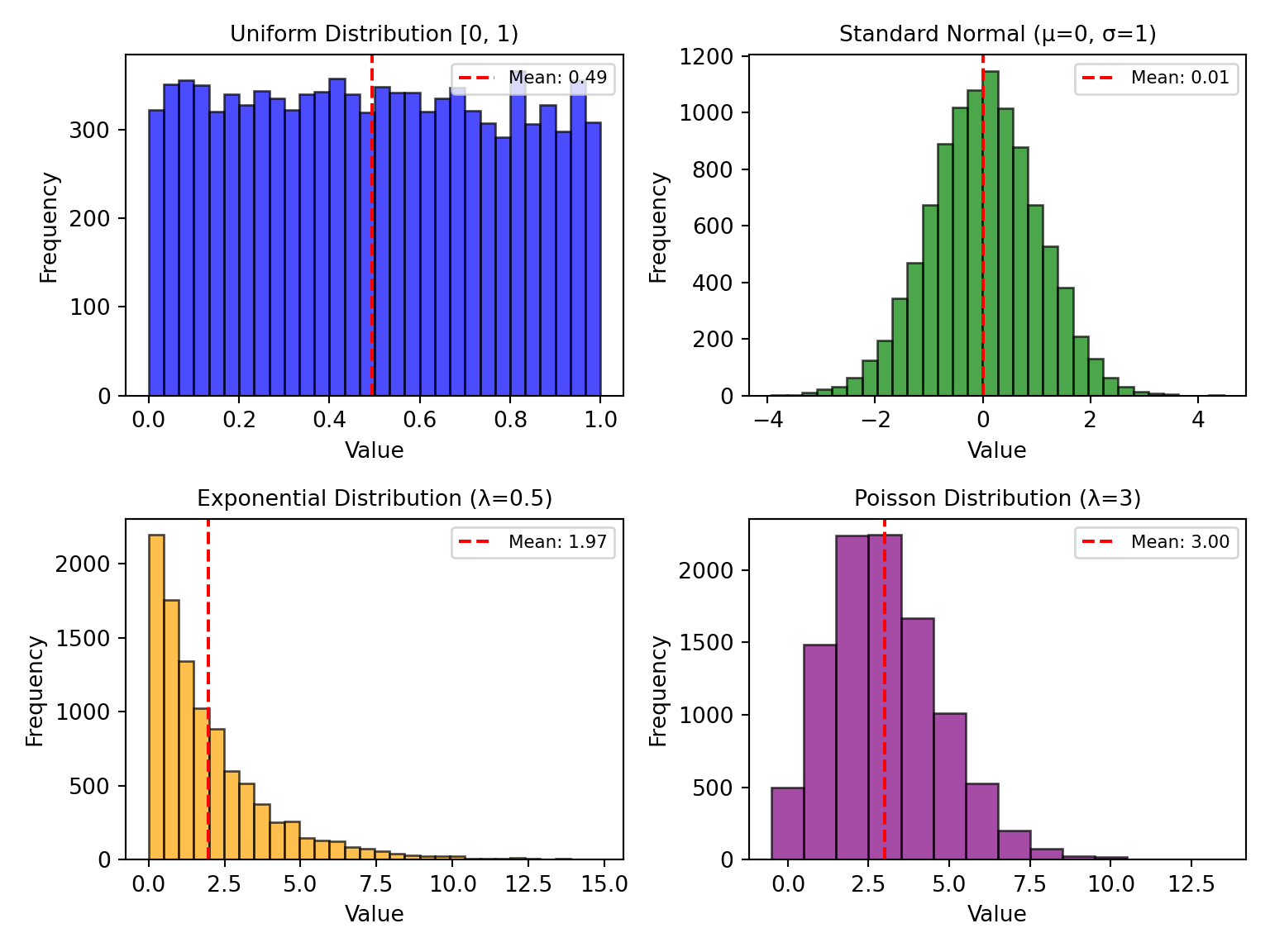
Reminder on Distributions

  • Uniform: All values equally likely (dice rolls, random sampling)
  • Normal: Bell curve, most common in nature (heights, measurement errors)
  • Exponential: Time between events (Exp(scale = 1/λ), e.g. insurance claim arrivals, If a policyholder files 0.2 claims per year on average → λ = 0.2, mean time between claims = 5 years)
  • Poisson: Count of events in fixed time (Pois(𝜆), e.g. number of claims per month, if 10 expected claims per month across a portfolio → λ = 10)

Why Random Numbers?

Random number generation has many usages. E.g. Monte Carlo simulations in risk assessment, Bootstrapping for confidence intervals, Synthetic data generation for testing, etc.

Interval Notation Explained

The notation [0, 1) uses mathematical interval notation:

  • [ (square bracket) = inclusive (includes the value)
  • ) (parenthesis) = exclusive (excludes the value)
  • Example: [0, 1) means: 0 ≤ x < 1 (includes 0, excludes 1)

🤔 Pop Quiz

Which of the following is true?

  • Arrays can contain elements of different data types
  • Arrays can only contain elements of the same data type
  • Arrays can only contain integers
  • Arrays can only contain floats

Array Attributes

Array Attributes

The attributes of a numpy array are:

  • ndim: number of dimensions (axes) of an array.
  • shape: tuple containing the size of an array in each dimension.
  • size: total number of elements in an array.
  • dtype: gives the data type of the elements of an array.
  • itemsize: provides the size (in bytes) of the elements of an array.

Key Differences

For an array with shape (3, 4) and dtype int64:

  • shape = (3, 4) → Structure: 3 rows × 4 columns
  • size = 12 → Total elements: 3 × 4 = 12 values
  • itemsize = 8 → Each element occupies 8 bytes (int64)
  • Total memory: size × itemsize = 12 × 8 = 96 bytes

🤔 Pop Quiz

For an array with shape (2, 3, 4), what is the total size?

  • 9 elements
  • 10 elements
  • 24 elements (2 × 3 × 4)
  • 234 elements

Indexing and Slicing

Note

Indexing and slicing are similar to Python lists but extended to multiple dimensions. Again, remember that indexing in Python starts at 0.

Warning

Arrays are mutable. meaning that changes modify the original (remember to use .copy() when needed!).

🤔 Pop Quiz

For a 2D array arr, what does arr[:, 1] select?

  • The first row
  • The second column (index 1)
  • The first column
  • A single element

Reshaping and Combining

Idea

How can we rearrange data without changing values?

🤔 Pop Quiz

Can you reshape an array of size 12 into shape (3, 5)?

  • Yes, NumPy will pad with zeros
  • Yes, NumPy will truncate extra elements
  • No, 3 × 5 = 15 ≠ 12
  • Yes, using -1 as a dimension

Vectorized Operations

Operator NumPy Function Description
+ np.add Addition
- np.subtract Subtraction
* np.multiply Multiplication
/ np.divide Division
** np.power Exponentiation
% np.mod Modulus

🤔 Pop Quiz

What does np.array([1, 2, 3]) * 2 produce?

  • An error
  • array([2, 4, 6])
  • array([1, 2, 3, 1, 2, 3])
  • 12

Aggregations

Idea

Aggregations are often used for summarizing data and doing some statstical analysis.

How

You must specify the axis along which the aggregate is computed

Claim Severity Analysis

Using gamma distribution to model claim amounts (common in actuarial practice)

🤔 Pop Quiz

For array [[1, 2], [3, 4]], what is arr.sum(axis=0)?

  • array([4, 6])
  • array([3, 7])
  • 10 - total sum
  • array([[4], [6]])

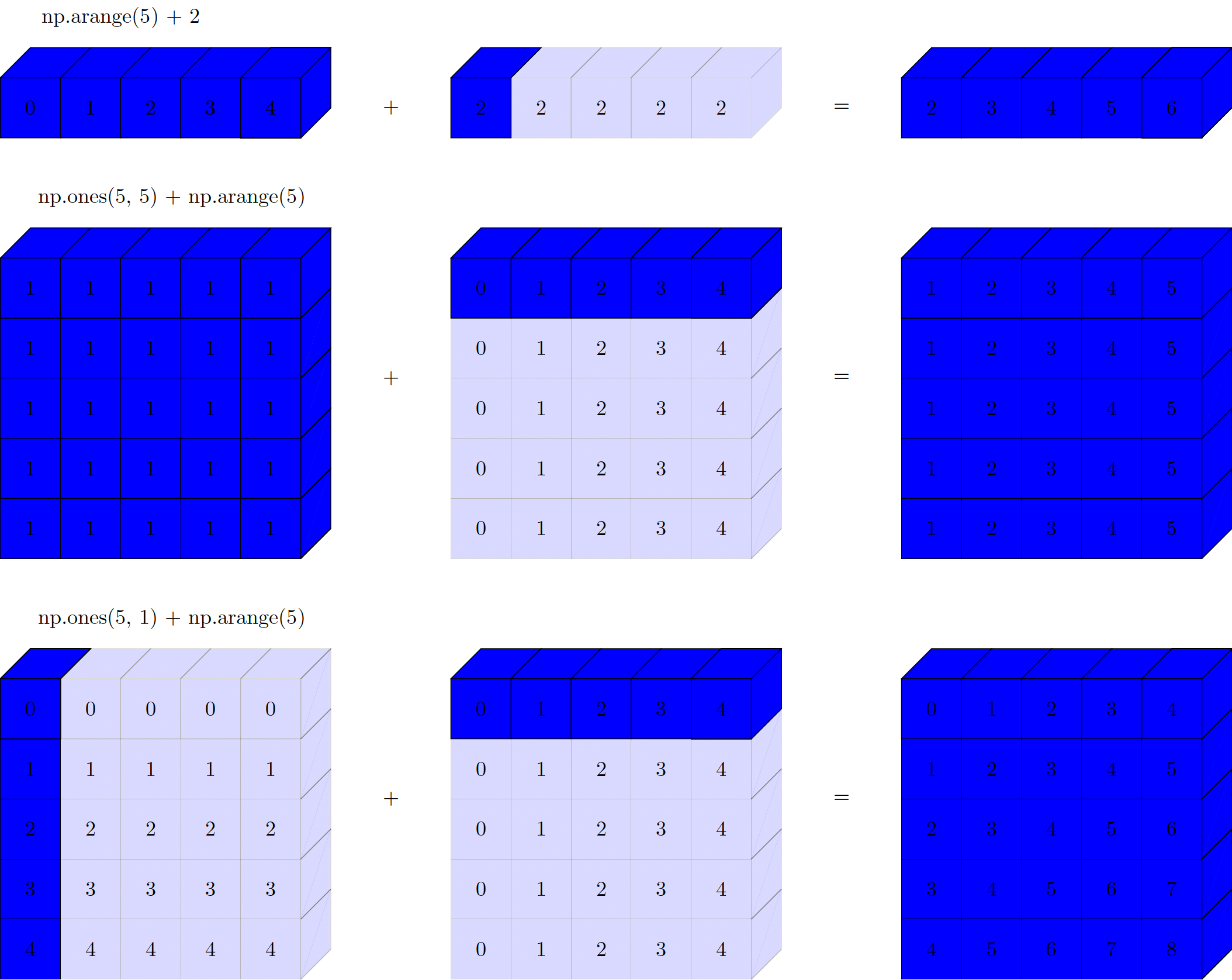
Broadcasting

Broadcasting is NumPy’s powerful mechanism for performing operations on arrays of different shapes.

Intuition

Think of it as “stretching” smaller arrays to match larger ones, enabling element-wise operations without explicit copying.

Broadcasting Rules

  1. Rule 1 (Padding): Arrays with fewer dimensions are padded with 1s on the left
    • Shape (3,) becomes (1, 3)
  2. Rule 2 (Stretching): Dimensions of size 1 are stretched to match the other array
    • Shape (1, 3) can stretch to (4, 3)
  3. Rule 3 (Compatibility): After rules 1 & 2, shapes must match exactly or error occurs
    • (3, 4) and (3, 4) ✓ Compatible
    • (3, 4) and (3, 5) ✗ Error!

What is this np.newaxis?

Simply put, numpy.newaxis is used to increase the dimension of the existing array by one more dimension, when used once. Thus:

  • 1D array will become 2D array
  • 2D array will become 3D array
  • 3D array will become 4D array
  • 4D array will become 5D array

🤔 Pop Quiz

Can arrays with shapes (3, 1) and (1, 4) be broadcast together?

  • Yes, resulting shape will be (3, 4)
  • No, incompatible shapes
  • Yes, resulting shape will be (3, 1)
  • Yes, resulting shape will be (1, 4)

Boolean Masks and Filtering

Idea

Create boolean arrays for filtering and analysis

Operator NumPy Function Description
& np.logical_and Element-wise AND
| np.logical_or Element-wise OR
~ np.logical_not Element-wise NOT

🤔 Pop Quiz

What does arr[arr > 5] return?

  • All indices where values are > 5
  • A 1D array of all values > 5
  • A boolean array
  • The count of values > 5

Advanced Indexing

Use arrays of indices to select multiple elements

🤔 Pop Quiz

For array [10, 20, 30, 40, 50], what does arr[[0, 2, 4]] return?

  • An error
  • array([10, 30, 50])
  • array([0, 2, 4])
  • array([10, 20, 30])

Sorting Arrays

Efficiency Tip

When you only need the k smallest/largest elements, use partition instead of full sorting. It’s O(n) vs O(n log n)!

NaN-Safe Operations

Common problem: Data that contains missing values

Standard NumPy functions propagate NaN values, potentially ruining calculations. Use NaN-safe versions when dealing with missing data!

Standard Function NaN-safe Version Description
np.sum np.nansum Sum ignoring NaNs
np.mean np.nanmean Mean ignoring NaNs
np.std np.nanstd Std deviation ignoring NaNs
np.var np.nanvar Variance ignoring NaNs
np.min np.nanmin Minimum ignoring NaNs
np.max np.nanmax Maximum ignoring NaNs
np.argmin np.nanargmin Index of min ignoring NaNs
np.argmax np.nanargmax Index of max ignoring NaNs
np.percentile np.nanpercentile Percentile ignoring NaNs
np.median np.nanmedian Median ignoring NaNs

🤔 Pop Quiz

What does np.nanmean([1, 2, np.nan, 4]) return?

  • NaN
  • An error
  • 2.333… (mean of 1, 2, 4)
  • 1.75 (treating NaN as 0)

Key Takeaways

  1. NumPy arrays are the foundation of numerical computing in Python

  2. Vectorization eliminates loops and speeds up calculations 10-100x

  3. Broadcasting enables flexible operations on different-shaped arrays

  4. Boolean indexing provides powerful data filtering capabilities

  5. Aggregations along axes enable sophisticated data analysis

  6. Integration with pandas, matplotlib, and scikit-learn creates complete workflow

One line takeaway

If you had to take away just one thing from this lecture, it would be: NumPy is not just about arrays, it’s about thinking in terms of vectorized operations and efficient numerical computing patterns that scale to real-world actuarial problems.

Questions?