flowchart LR
%% Main linear flow
Acquire --> Tidy
Tidy --> Transform
%% Circular connections between Transform, Visualize, and Model
Transform <--> Visualize
Visualize <--> Model
Model <--> Transform
%% Final connections to Communicate
%% Visualize --> Communicate
Model --> Communicate
%% Styling for clean appearance
classDef default fill:#ffffff,stroke:#000000,stroke-width:2px,color:#000000,font-family:Arial,font-size:14px
class Acquire,Tidy,Transform,Visualize,Model,Communicate default
Data Science Pipeline
MScAS 2025 - DSAS Lecture 5
2025-10-21
From Theory to Practice
Course Overview
You’ve learned Python, NumPy, Pandas, and Visualization. Today we apply these tools to real actuarial problems using a complete data science workflow.
What we’ll cover:
- The Data Science Workflow - Complete pipeline from data acquisition to communication
- Case Study: Health Insurance EDA - Brief exploratory data analysis example
- Case Study: Interest Rate Analysis - Dimensionality reduction with PCA
Tip
Everything today applies directly to your course project (due November 12th)
The Data Science Workflow
| Stage | What it means | Actuarial example |
|---|---|---|
| Acquire | Get data from external/internal sources | Download claims data from database or regulator website |
| Tidy | Clean, format, handle missing values | Fix date formats, remove duplicates, handle NaN values |
| Transform | Create new variables, normalize | Calculate BMI categories, create age bands |
| Visualize | Explore patterns, spot issues | Histograms of claims, scatter plots of age vs. premium |
| Model | Apply statistical/ML methods | Fit GLM, perform PCA, cluster risk groups |
| Communicate | Share findings with stakeholders | Write report, create presentation, explain insights |
It’s Iterative, Not Linear
Data science is messy. You’ll loop through these steps multiple times before completing your analysis.
Garbage In, Garbage Out (GIGO)
Bad data + good analysis = worthless results
The foundation of any project is data quality. Don’t skip the cleaning step!
Signs of Bad Data:
- Unknown/untrusted source
- Many missing values (>20%)
- Implausible values (age = -5)
- Inconsistent formats
- Duplicates
- No documentation
Signs of Good Data:
- Trusted source (regulator, internal)
- Complete records
- Validated values
- Consistent formatting
- Unique records
- Clear data dictionary
Pop Quiz
Data scientists spend 80% of time on data wrangling, 20% on modeling. Why does this persist despite automations?
- Modern libraries have solved most data preparation challenges
- GIGO: Model sophistication cannot compensate for poor data quality; it requires domain-specific human judgment
- Data scientists lack proper training in efficient preprocessing
- Companies create complicated pipelines to justify larger teams
Case Study I: Health Insurance
The Scenario
You’re the appointed actuary of a US health insurer. Before estimating technical provisions, you need to conduct an EDA of the portfolio.
Dataset: healthinsurance.csv with 1,338 clients
Your mission
Discover patterns and relationships to understand the portfolio’s risk profile
| Variable | Description |
|---|---|
age |
Age of primary beneficiary (years) |
sex |
Gender: male or female |
bmi |
Body Mass Index |
children |
Number of dependents covered |
smoker |
Smoking status: yes or no |
region |
US region: northeast, northwest, southeast, southwest |
charges |
Annual medical costs billed ($) |
EDA Steps
Overview
1,338 clients × 7 variables | No missing values | Ready to analyze!
Key findings
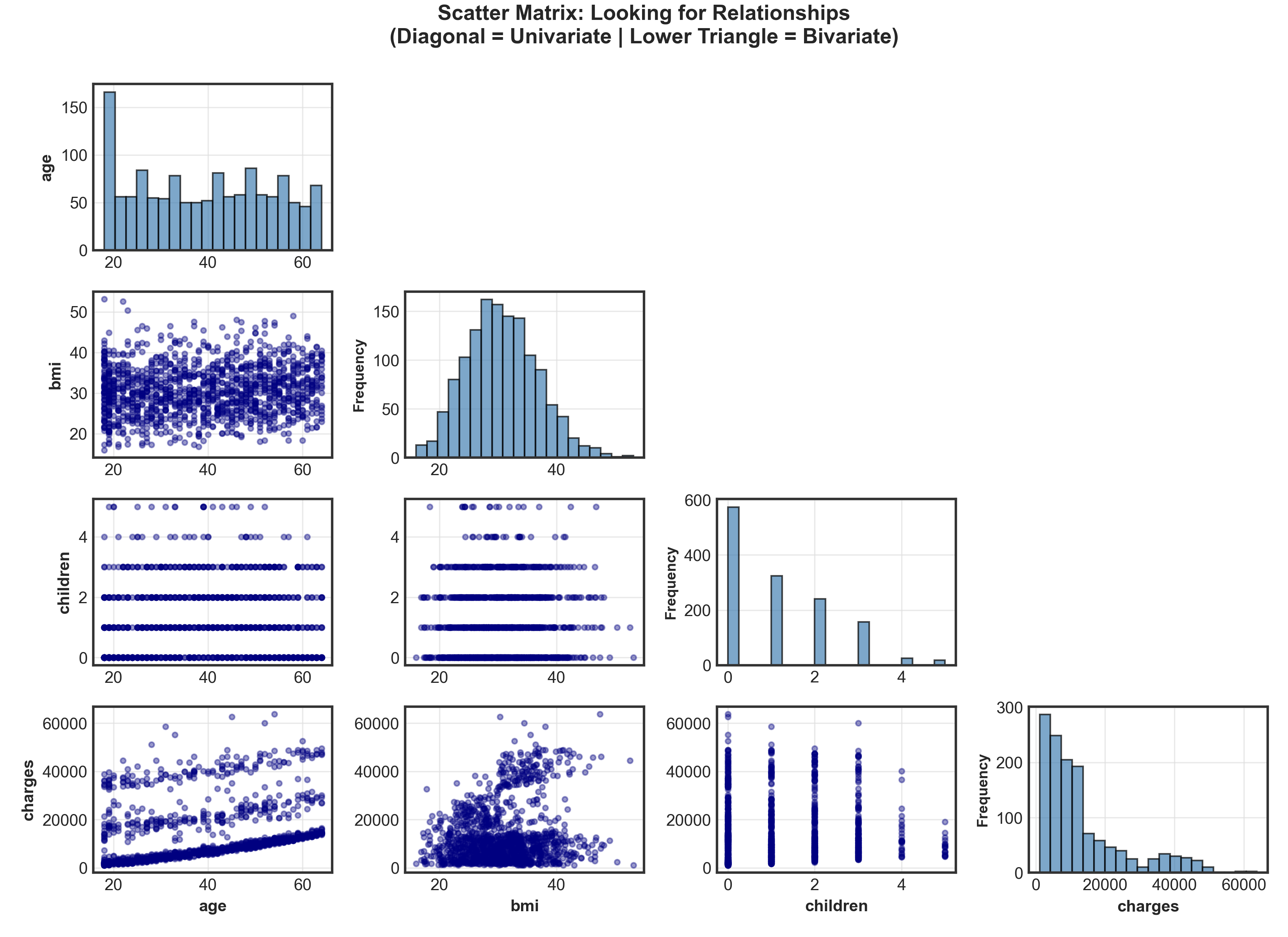
Age 18-64 | BMI mean=30.7 (overweight) | Charges: very significant range $1K-$64K!
Show code
# Load data for visualization
data = pd.read_csv('healthinsurance.csv')
# Create scatter matrix with custom layout
variables = ['age', 'bmi', 'children', 'charges']
n_vars = len(variables)
fig, axes = plt.subplots(n_vars, n_vars, figsize=(11, 8))
for i in range(n_vars):
for j in range(n_vars):
ax = axes[i, j]
if i == j: # Diagonal: univariate distributions
ax.hist(data[variables[i]], bins=20, alpha=0.7, color='steelblue', edgecolor='black')
ax.set_ylabel('Frequency', fontsize=9, fontweight='bold')
elif i > j: # Lower triangle: bivariate scatter plots
ax.scatter(data[variables[j]], data[variables[i]], alpha=0.4, s=10, color='navy')
ax.set_xlabel(variables[j] if i == n_vars-1 else '', fontsize=9)
ax.set_ylabel(variables[i] if j == 0 else '', fontsize=9)
else: # Upper triangle: hide
ax.axis('off')
# Add labels to leftmost column and bottom row
for i in range(n_vars):
axes[i, 0].set_ylabel(variables[i], fontsize=10, fontweight='bold')
axes[n_vars-1, i].set_xlabel(variables[i], fontsize=10, fontweight='bold')
plt.suptitle("Scatter Matrix: Looking for Relationships\n(Diagonal = Univariate | Lower Triangle = Bivariate)",
fontsize=13, fontweight='bold', y=0.995)
plt.tight_layout()
plt.show()Warning
Suspicious pattern spotted! Age vs. Charges shows 3 distinct groups → not random scatter!
Diving Deeper: Risk Factors
Show code
fig, axes = plt.subplots(1, 2, figsize=(10, 4.5))
# Histogram of age
_ = axes[0].hist(data['age'], bins=47, edgecolor='black', alpha=0.75, color='steelblue')
_ = axes[0].set_title("Age Distribution", fontsize=12, fontweight='bold')
_ = axes[0].set_xlabel("Age (years)", fontsize=10)
_ = axes[0].set_ylabel("Frequency", fontsize=10)
_ = axes[0].grid(True, alpha=0.3, axis='y')
# Scatter plot: Age vs Charges
_ = axes[1].scatter(data['age'], data['charges'], alpha=0.5, s=30, color='coral', edgecolors='black', linewidth=0.3)
_ = axes[1].set_title("Age vs. Annual Charges", fontsize=12, fontweight='bold')
_ = axes[1].set_xlabel("Age (years)", fontsize=10)
_ = axes[1].set_ylabel("Charges ($)", fontsize=10)
_ = axes[1].grid(True, alpha=0.3)
plt.tight_layout()
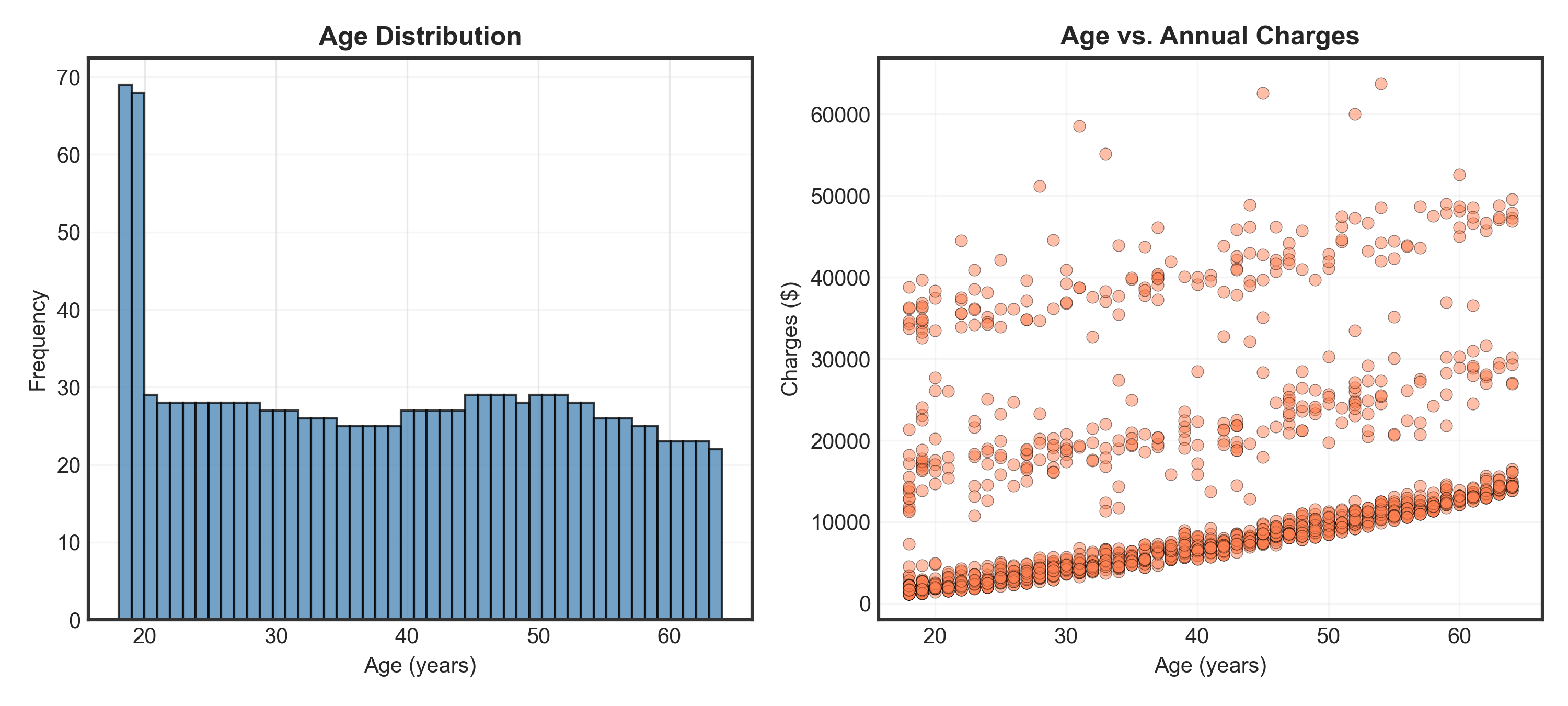
plt.show()Observations
- Age: Nearly uniform distribution (except spike at 18-19 years)
- Charges: Clear 3-tier structure → low, medium, and high-cost groups! What explains this?
Show code
# Calculate percentages
smoker_counts = data.groupby('smoker').size()
total = len(data)
pct_smoker = (smoker_counts['yes'] / total) * 100
pct_nonsmoker = (smoker_counts['no'] / total) * 100
# Create scatter plot
fig, ax = plt.subplots(figsize=(10, 4.5))
colors = {'yes': 'orange', 'no': 'purple'}
for smoker_status in ['yes', 'no']:
mask = data['smoker'] == smoker_status
label = f"Smoker ({pct_smoker:.1f}%)" if smoker_status == 'yes' else f"Non-smoker ({pct_nonsmoker:.1f}%)"
_ = ax.scatter(data.loc[mask, 'age'],
data.loc[mask, 'charges'],
c=colors[smoker_status],
label=label,
alpha=0.6, s=35, edgecolors='black', linewidth=0.3)
_ = ax.set_title("Age vs. Charges (by Smoking Status)", fontsize=13, fontweight='bold')
_ = ax.set_xlabel("Age (years)", fontsize=11)
_ = ax.set_ylabel("Charges ($)", fontsize=11)
_ = ax.legend(fontsize=10, loc='upper left')
_ = ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()Warning
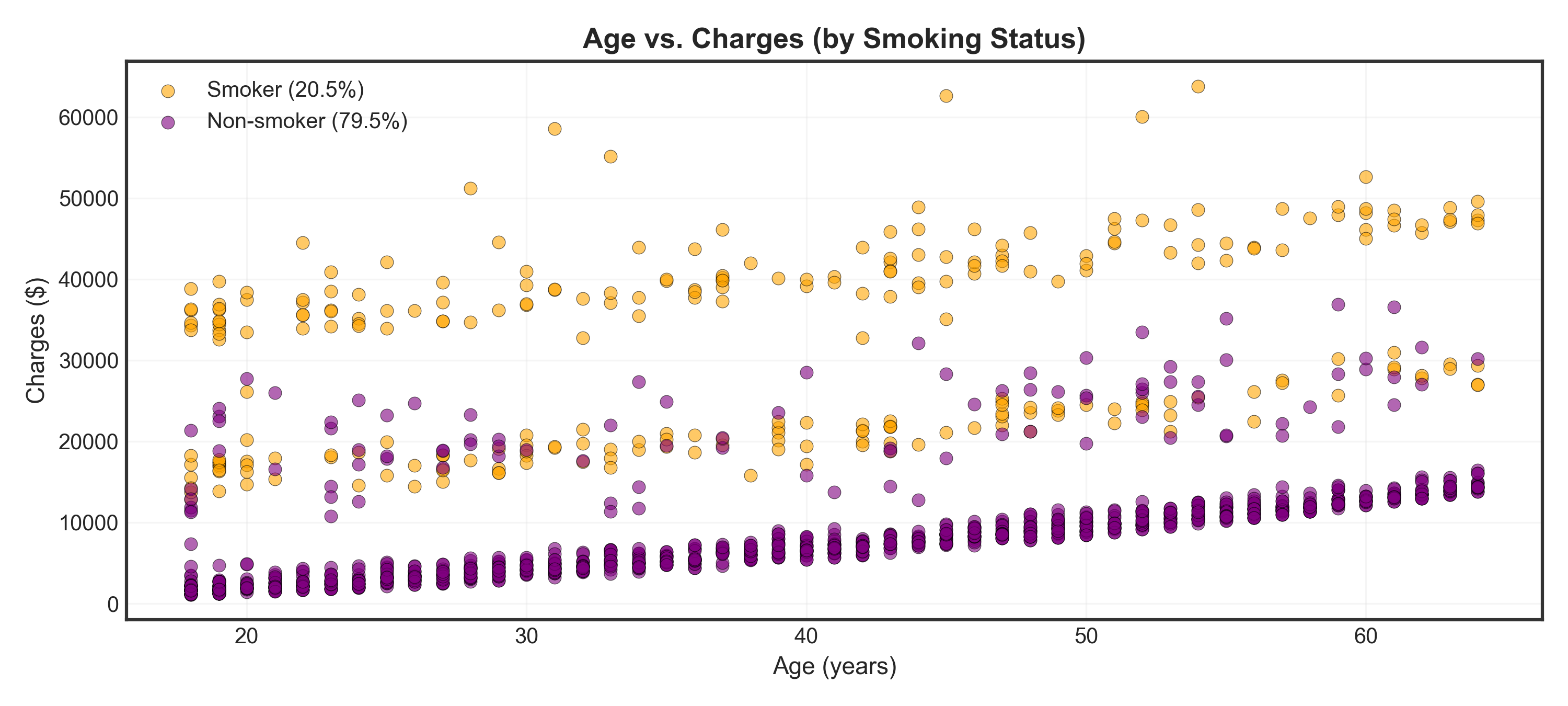
Major finding: Smokers (orange) have dramatically higher charges than non-smokers (purple) across all ages!
Show code
# --- Setup Labels ---
# 1. Define short labels for the data column and dictionary keys
short_labels = ['Underweight', 'Healthy', 'Overweight', 'Obesity', 'Severe Obesity']
# 2. Define the long, descriptive labels you want in the legend
long_labels = ['Underweight: BMI < 18.5',
'Healthy: 18.5 ≤ BMI < 25',
'Overweight: 25 ≤ BMI < 30',
'Obesity: 30 ≤ BMI < 40',
'Severe Obesity: BMI ≥ 40']
# 3. Create a "map" to link them
label_map = dict(zip(short_labels, long_labels))
# 4. Define your colors using the SHORT labels
colors_bmi = {'Underweight': 'lightblue',
'Healthy': 'green',
'Overweight': 'yellow',
'Obesity': 'orange',
'Severe Obesity': 'red'}
# --- Create BMI categories ---
# Use the SHORT labels to create the data column
data['NHS_BMI'] = pd.cut(data['bmi'],
bins=[0, 18.5, 25, 30, 40, 100],
labels=short_labels)
# --- Visualization ---
fig, ax = plt.subplots(figsize=(10, 4.5))
# Loop through the SHORT labels in REVERSE order (highest to lowest BMI)
for bmi_cat in reversed(short_labels):
mask = data['NHS_BMI'] == bmi_cat
# Skip if this category has no data (prevents errors)
if not mask.any():
continue
_ = ax.scatter(data.loc[mask, 'age'],
data.loc[mask, 'charges'],
c=colors_bmi[bmi_cat], # Uses the short label (e.g., 'Overweight')
label=label_map[bmi_cat], # Uses the map to get the long label (e.g., 'Overweight: 25 ≤ BMI < 30')
alpha=0.6, s=30, edgecolors='black', linewidth=0.3)
_ = ax.set_title("Age vs. Charges (by BMI Category)", fontsize=13, fontweight='bold')
_ = ax.set_xlabel("Age (years)", fontsize=11)
_ = ax.set_ylabel("Charges ($)", fontsize=11)
_ = ax.legend(fontsize=9, loc='upper left')
_ = ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()Tip
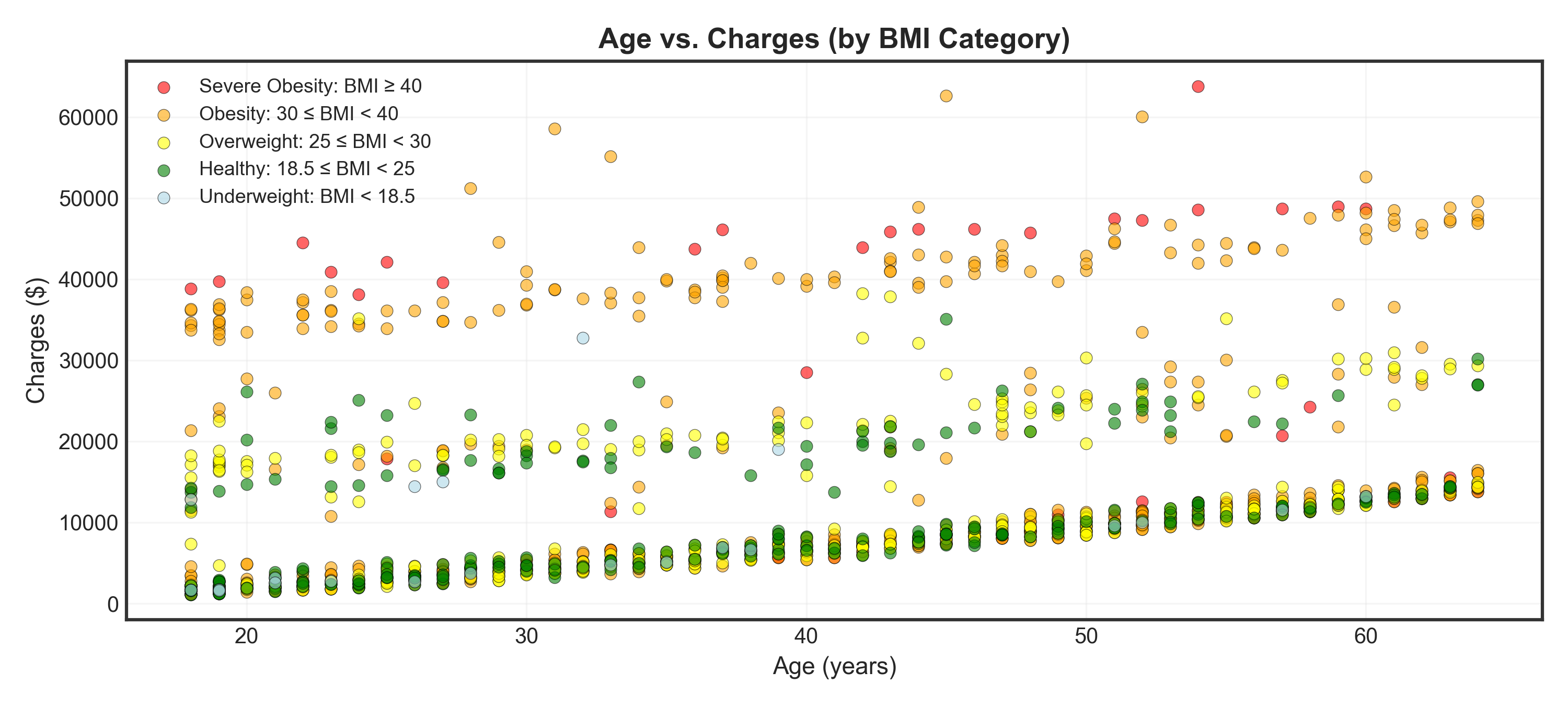
Insight: Higher BMI categories (especially severe obesity) cluster in the high-charge regions
Show code
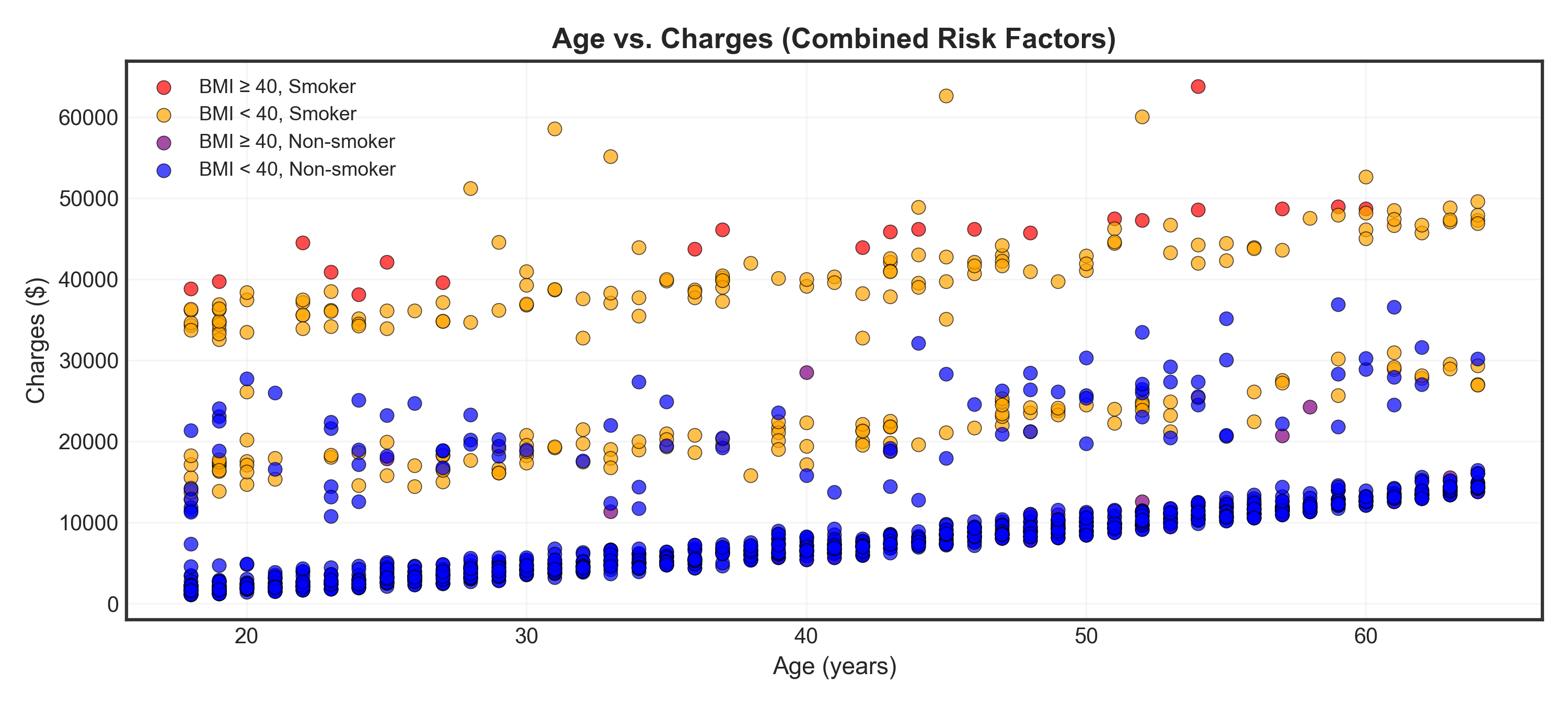
# Create combined category
data['BMI_Smoker'] = 'BMI < 40, Non-smoker'
data.loc[(data['bmi'] >= 40) & (data['smoker'] == 'no'), 'BMI_Smoker'] = 'BMI ≥ 40, Non-smoker'
data.loc[(data['bmi'] < 40) & (data['smoker'] == 'yes'), 'BMI_Smoker'] = 'BMI < 40, Smoker'
data.loc[(data['bmi'] >= 40) & (data['smoker'] == 'yes'), 'BMI_Smoker'] = 'BMI ≥ 40, Smoker'
# Visualization
fig, ax = plt.subplots(figsize=(10, 4.5))
# Define colors and order from highest to lowest risk
colors_combined = {
'BMI ≥ 40, Smoker': 'red',
'BMI < 40, Smoker': 'orange',
'BMI ≥ 40, Non-smoker': 'purple',
'BMI < 40, Non-smoker': 'blue'
}
for category in colors_combined.keys():
mask = data['BMI_Smoker'] == category
_ = ax.scatter(data.loc[mask, 'age'],
data.loc[mask, 'charges'],
c=colors_combined[category],
label=category,
alpha=0.7, s=40, edgecolors='black', linewidth=0.4)
_ = ax.set_title("Age vs. Charges (Combined Risk Factors)", fontsize=13, fontweight='bold')
_ = ax.set_xlabel("Age (years)", fontsize=11)
_ = ax.set_ylabel("Charges ($)", fontsize=11)
_ = ax.legend(fontsize=9, loc='upper left', framealpha=0.9)
_ = ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()Warning
Critical finding: High BMI (≥40) + Smoking (red points) = highest charges regardless of age!
🤔 Pop Quiz
Based on the visualizations, which group likely has the HIGHEST average charges?
- Young non-smokers with healthy BMI
- Elderly non-smokers with high BMI
- Elderly smokers with severe obesity
- Middle-aged non-smokers with children
Case Study I: EDA Key Takeaways
What We Discovered Through EDA
- 3-tier charge structure driven by risk factors
- Smoking is the strongest predictor of high charges
- High BMI (≥40) amplifies the smoking effect
- Age matters, but lifestyle matters more
- Combination effects are more important than individual factors
For the insurer: Risk-based pricing should heavily weight smoking status and BMI!
The EDA Process
- ✅ Load data
- ✅ Check quality
- ✅ Summary stats
- ✅ Visualize patterns
- ✅ Investigate anomalies
- ✅ Draw insights
This is very similar to what you’ll do for your project!
Case Study II: Interest Rate Analysis
Swiss National Bank Yield Data
Scenario: Analyzing Swiss government bond yields for risk management.
Dataset shape: 329 observations × 14 variables
| date | 1M | 2M | 3M | 6M | 1J | 2J | 3J | 4J | 5J | 6J | 7J | 8J | 9J |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1997-12 | 1.658 | 1.883 | 2.136 | 2.384 | 2.614 | 2.821 | 3.006 | 3.171 | 3.316 | 3.445 | 3.903 | 4.167 | 4.445 |
| 1998-01 | 1.407 | 1.583 | 1.809 | 2.039 | 2.256 | 2.455 | 2.636 | 2.801 | 2.949 | 3.084 | 3.593 | 3.917 | 4.284 |
| 1998-02 | 1.128 | 1.369 | 1.619 | 1.860 | 2.084 | 2.291 | 2.481 | 2.656 | 2.816 | 2.964 | 3.543 | 3.936 | 4.408 |
| 1998-03 | 1.568 | 1.758 | 1.946 | 2.131 | 2.313 | 2.488 | 2.657 | 2.817 | 2.968 | 3.109 | 3.680 | 4.065 | 4.510 |
| 1998-04 | 1.715 | 1.981 | 2.205 | 2.403 | 2.585 | 2.756 | 2.916 | 3.068 | 3.211 | 3.344 | 3.888 | 4.255 | 4.677 |
| 1998-05 | 1.720 | 1.921 | 2.111 | 2.291 | 2.461 | 2.622 | 2.773 | 2.916 | 3.051 | 3.179 | 3.722 | 4.137 | 4.712 |
| 1998-06 | 2.117 | 2.216 | 2.333 | 2.466 | 2.608 | 2.754 | 2.899 | 3.041 | 3.178 | 3.308 | 3.851 | 4.228 | 4.674 |
| 1998-07 | 1.982 | 2.067 | 2.198 | 2.347 | 2.499 | 2.649 | 2.794 | 2.932 | 3.064 | 3.190 | 3.722 | 4.120 | 4.641 |
Column naming
J = Jahre (years), M = Monate (months) so 1J = 1-year, 2J = 2-year and 1M = 1-month, 6M = 6-month
Show code
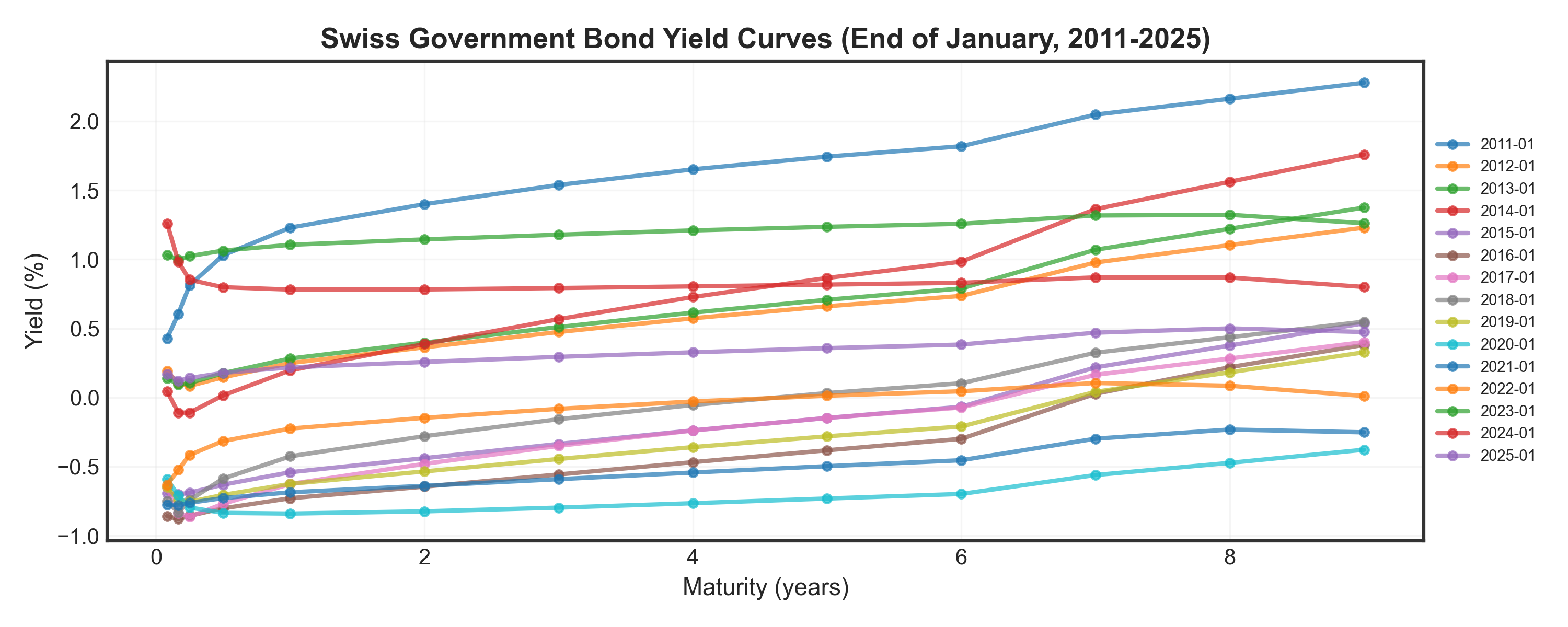
# Plot yield curves over time
fig, ax = plt.subplots(figsize=(10, 4))
months = [str(i) + "-01" for i in range(2011, 2026)] # Every year, January
for month in months:
if month in df['date'].values:
yields = df.loc[df['date'] == month, df.columns[1:]].values.flatten()
_ = ax.plot(maturities, yields, marker='o', linewidth=2, markersize=4, alpha=0.7, label=month)
_ = ax.set_title("Swiss Government Bond Yield Curves (End of January, 2011-2025)", fontsize=13, fontweight='bold')
_ = ax.set_xlabel("Maturity (years)", fontsize=11)
_ = ax.set_ylabel("Yield (%)", fontsize=11)
_ = ax.legend(fontsize=7, loc='center left', bbox_to_anchor=(1, 0.5))
_ = ax.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()🤔 Pop Quiz
Looking at the dataset shape, we have 329 observations. What does each observation represent?
- A different bond maturity (1Y, 2Y, 3Y, etc.)
- A different type of Swiss government bond
- A different month (monthly data from ~1997 to 2024)
- A different country’s yield curve
The Correlation Problem
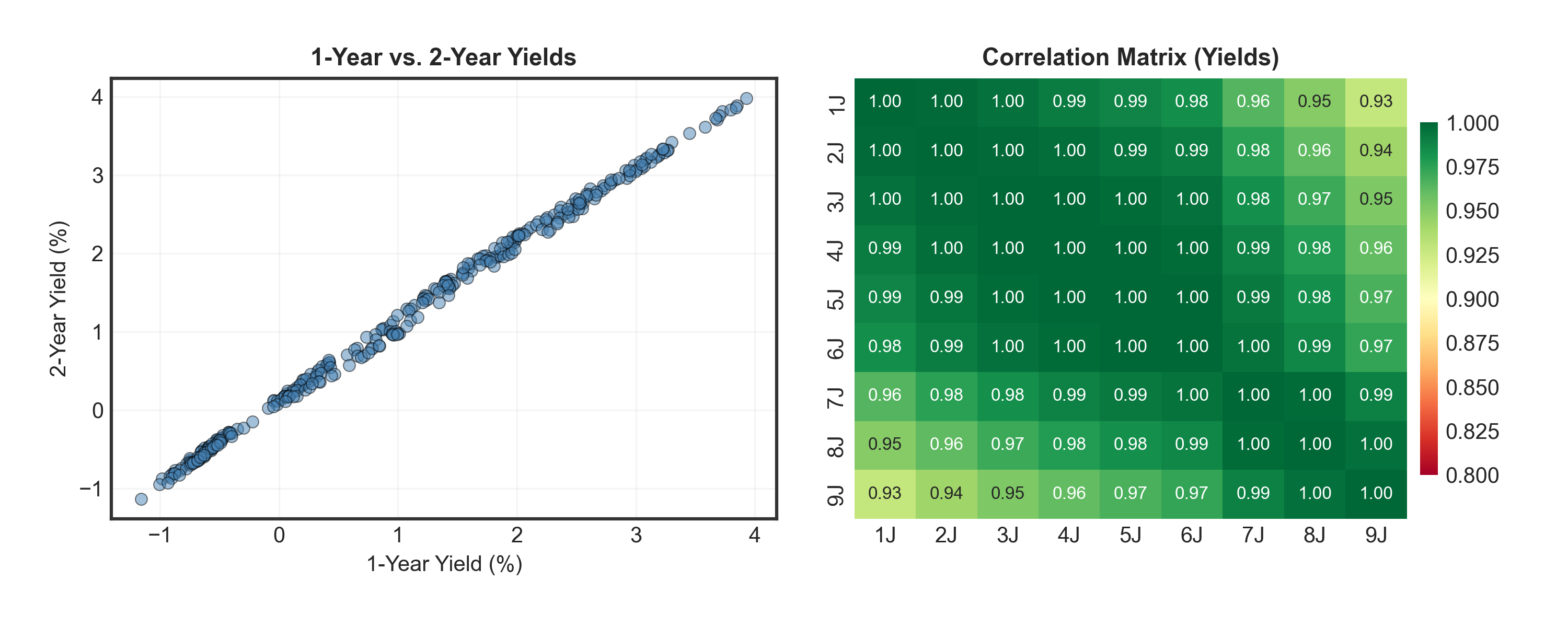
Show code
fig, axes = plt.subplots(1, 2, figsize=(10, 4))
# Scatter plot: 1Y vs 2Y yields
_ = axes[0].scatter(df['1J'], df['2J'], alpha=0.5, s=30, color='steelblue', edgecolors='black', linewidth=0.5)
_ = axes[0].set_title("1-Year vs. 2-Year Yields", fontsize=11, fontweight='bold')
_ = axes[0].set_xlabel("1-Year Yield (%)", fontsize=10)
_ = axes[0].set_ylabel("2-Year Yield (%)", fontsize=10)
_ = axes[0].grid(True, alpha=0.3)
# Correlation heatmap
corr = df.iloc[:, 5:].corr() # Use only yearly maturities for clarity
_ = sns.heatmap(corr, annot=True, fmt=".2f", cmap="RdYlGn", ax=axes[1],
cbar_kws={'shrink': 0.8, 'pad': 0.02}, vmin=0.8, vmax=1,
annot_kws={'size': 8})
_ = axes[1].set_title("Correlation Matrix (Yields)", fontsize=11, fontweight='bold')
plt.tight_layout(pad=2.0)
plt.show()Warning
Problem: All yields are highly correlated (0.90-0.99)! We have redundant information across many maturities (1M, 2M, 3M, 6M, 1Y, 2Y, …, 9Y).
Solution: Use Principal Component Analysis (PCA) to find the key patterns and reduce to just a few key variables!
What is PCA?
Principal Component Analysis: Dimensionality Reduction
Goal: Transform correlated variables into a smaller set of uncorrelated components that capture most of the variation.
Key idea: Find new axes (principal components) that explain maximum variance in the data.
Before PCA:
- +10 variables
- All correlated (0.90-0.99)
- Redundant information
- Hard to visualize
After PCA:
- 2-3 principal components
- Uncorrelated by design
- 99% of variance retained
- Easy to interpret & visualize
Analogy
An insurer tracks +20 variables for each claim: age, gender, job type, car brand, engine size, annual mileage, parking type, claims history, etc.
After analysis, you discover that 3 key factors explain most claims:
- driver experience (age + claims history),
- vehicle risk (car brand + engine size), and
- exposure (annual mileage + parking type).
PCA does exactly this—it finds the few combined factors that capture (almost) all the risk!
PCA: Steps
Step 1: Normalize Data
- Convert all variables to same scale (mean=0, std=1)
- Formula: \(z_{ij} = \frac{x_{ij} - \mu_j}{\sigma_j}\)
Step 2: Compute Principal Components
- Calculate covariance matrix: \(\mathbf{\Sigma} = \frac{1}{n-1}\mathbf{X}^T\mathbf{X}\)
- Find eigenvectors & eigenvalues: \(\mathbf{\Sigma} \mathbf{v}_k = \lambda_k \mathbf{v}_k\)
- \(\mathbf{v}_k\) are eigenvectors representing the directions of principal components (the “weights”)
- \(\lambda_k\) are eigenvalues, showing the variance explained by each component
- Sort by eigenvalues (largest = most variance explained)
Step 3: Interpret Components
- PC1 (largest \(\lambda_1\) ): Captures most variance → “Level”
- PC2 (second \(\lambda_2\) ): Next most variance → “Slope” etc.
Step 4: Transform & Reconstruct
- Project data: \(\mathbf{Z} = \mathbf{X} \cdot \mathbf{V}\) (PC scores)
- Reconstruct: \(\hat{\mathbf{X}} = \mathbf{Z}_K \cdot \mathbf{V}_K^T\) (using top K components)
Key Insights
- Total variance: First few components (K=2-3) typically capture 95-99% of total variance!
- Implementation: In practice, we can use
sklearn.decomposition.PCAfrom scikit-learn.
Why Normalize?
Variables with different scales would dominate PCA. Standardization ensures equal contribution, giving each variable mean = 0 and std = 1.
Finding Principal Components
Compute the covariance matrix, find its eigenvectors (PC directions) and eigenvalues (variance explained), then sort by importance.
Tip
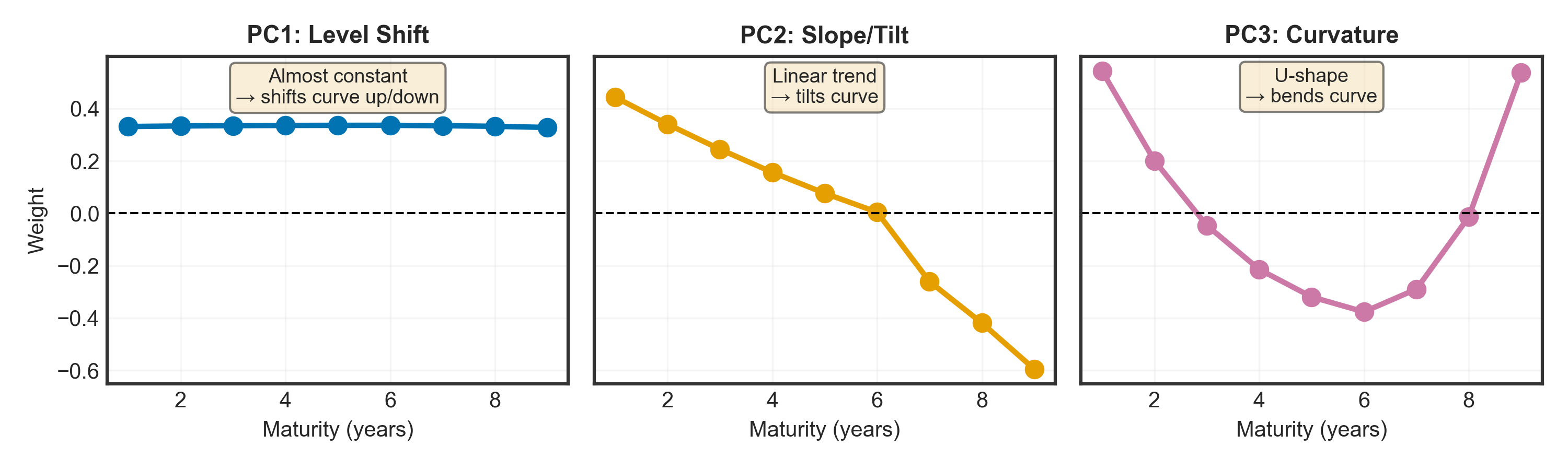
Key insight: First 3 components explain >99% of variation! We can safely ignore the rest.
Understanding “Weights”
The weights (eigenvector values) tell us how much each maturity contributes when a principal component changes:
- Each yield curve = weighted combination of PC1 + PC2 + PC3
- Weights = the multipliers for each maturity when that component is “activated”
- Example: If PC1 = 2.0 and 1Y weight = 0.33, then PC1 contributes 2.0 × 0.33 = 0.66% to the 1Y yield
Show code
# Prepare data
df_yields = df.iloc[:, 5:] # Use only yearly maturities
mean = df_yields.mean()
std = df_yields.std()
df_norm = (df_yields - mean) / std
# Compute PCA
cov_matrix = df_norm.cov()
eigen_values, eigen_vectors = np.linalg.eig(cov_matrix)
sorted_idx = np.argsort(eigen_values)[::-1]
eigen_vectors = eigen_vectors[:, sorted_idx]
# Get first 3 PCs - make maturities list dynamic based on actual data
maturities = list(range(1, len(df_yields.columns) + 1))
pc1 = eigen_vectors[:, 0]
pc2 = eigen_vectors[:, 1]
pc3 = eigen_vectors[:, 2]
# Print actual weights for PC1 to show they're approximately equal
print("PC1 weights (1Y-9Y):", np.round(pc1, 3))
print("Theoretical equal weight for 9 variables:", np.round(1/np.sqrt(9), 3))
print("\nVerification - Each PC is normalized to length 1:")
print(f"PC1 norm: {np.linalg.norm(pc1):.6f}")
print(f"PC2 norm: {np.linalg.norm(pc2):.6f}")
print(f"PC3 norm: {np.linalg.norm(pc3):.6f}")
print("\nCross-PC sum for 1Y maturity (NOT constrained to 1):")
print(f"PC1[1Y] + PC2[1Y] + PC3[1Y] = {pc1[0]:.3f} + {pc2[0]:.3f} + {pc3[0]:.3f} = {pc1[0] + pc2[0] + pc3[0]:.3f}")
# Example reconstruction for first observation
print("\nExample: Reconstructing 1Y yield for first date:")
pc_scores = df_norm.dot(eigen_vectors)
first_date_1y_norm = pc_scores.iloc[0, 0] * pc1[0] + pc_scores.iloc[0, 1] * pc2[0] + pc_scores.iloc[0, 2] * pc3[0]
first_date_1y_actual = df_norm.iloc[0, 0]
print(f" PC1_score × PC1_weight[1Y] + PC2_score × PC2_weight[1Y] + PC3_score × PC3_weight[1Y]")
print(f" = {pc_scores.iloc[0, 0]:.3f} × {pc1[0]:.3f} + {pc_scores.iloc[0, 1]:.3f} × {pc2[0]:.3f} + {pc_scores.iloc[0, 2]:.3f} × {pc3[0]:.3f}")
print(f" = {first_date_1y_norm:.3f}")
print(f" Actual normalized 1Y yield: {first_date_1y_actual:.3f}")
print(f" Match: {np.isclose(first_date_1y_norm, first_date_1y_actual)}")
# Plot
fig, axes = plt.subplots(1, 3, figsize=(10, 3), sharey=True)
_ = axes[0].plot(maturities, pc1, marker='o', linewidth=2.5, markersize=8, color='#0173B2')
_ = axes[0].axhline(y=0, color='black', linestyle='--', linewidth=1)
_ = axes[0].set_title("PC1: Level Shift", fontsize=11, fontweight='bold')
_ = axes[0].set_xlabel("Maturity (years)", fontsize=10)
_ = axes[0].set_ylabel("Weight", fontsize=10)
_ = axes[0].grid(True, alpha=0.3)
_ = axes[0].text(5, max(pc1)*1.25, "Almost constant\n→ shifts curve up/down",
ha='center', fontsize=9, bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5))
_ = axes[1].plot(maturities, pc2, marker='o', linewidth=2.5, markersize=8, color='#E69F00')
_ = axes[1].axhline(y=0, color='black', linestyle='--', linewidth=1)
_ = axes[1].set_title("PC2: Slope/Tilt", fontsize=11, fontweight='bold')
_ = axes[1].set_xlabel("Maturity (years)", fontsize=10)
_ = axes[1].grid(True, alpha=0.3)
_ = axes[1].text(5, max(pc2)*0.95, "Linear trend\n→ tilts curve",
ha='center', fontsize=9, bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5))
_ = axes[2].plot(maturities, pc3, marker='o', linewidth=2.5, markersize=8, color='#CC79A7')
_ = axes[2].axhline(y=0, color='black', linestyle='--', linewidth=1)
_ = axes[2].set_title("PC3: Curvature", fontsize=11, fontweight='bold')
_ = axes[2].set_xlabel("Maturity (years)", fontsize=10)
_ = axes[2].grid(True, alpha=0.3)
_ = axes[2].text(5, max(pc3)*0.78, "U-shape\n→ bends curve",
ha='center', fontsize=9, bbox=dict(boxstyle='round', facecolor='wheat', alpha=0.5))
plt.tight_layout()
plt.show()What Do These Components Actually Mean?
PC1: Level Shift (~98.44% of variance)
- Weights: All maturities ≈ 0.33 (almost equal and positive)
- Interpretation: All yields move together by the same amount
- When PC1 score increases by 1 → ALL rates shift up by ~0.33% in parallel
- Real example: Central bank raises policy rate → entire curve moves up together (inflation shock)
PC2: Slope/Tilt (~1.46% of variance)
- Weights: Short-term: positive (+0.4) | Long-term: negative (-0.6)
- Interpretation: Short and long rates move in opposite directions
- When PC2 score increases → short rates ↑ & long rates ↓ → curve flattens
- Real example: Recession fears → long rates drop (expect rate cuts), short rates stay high
PC3: Curvature (~0.09% of variance)
- Weights: Ends: positive | Middle (4-6Y): negative
- Interpretation: Middle maturities move opposite to short/long ends
- When PC3 score increases → middle bends down, ends bend up → humped curve
- Real example: Expect rates to rise then fall → medium-term rates peak
In simple terms: PC1 score = “How high is the curve?”, PC2 score = “How steep?”, PC3 score = “How curved?”
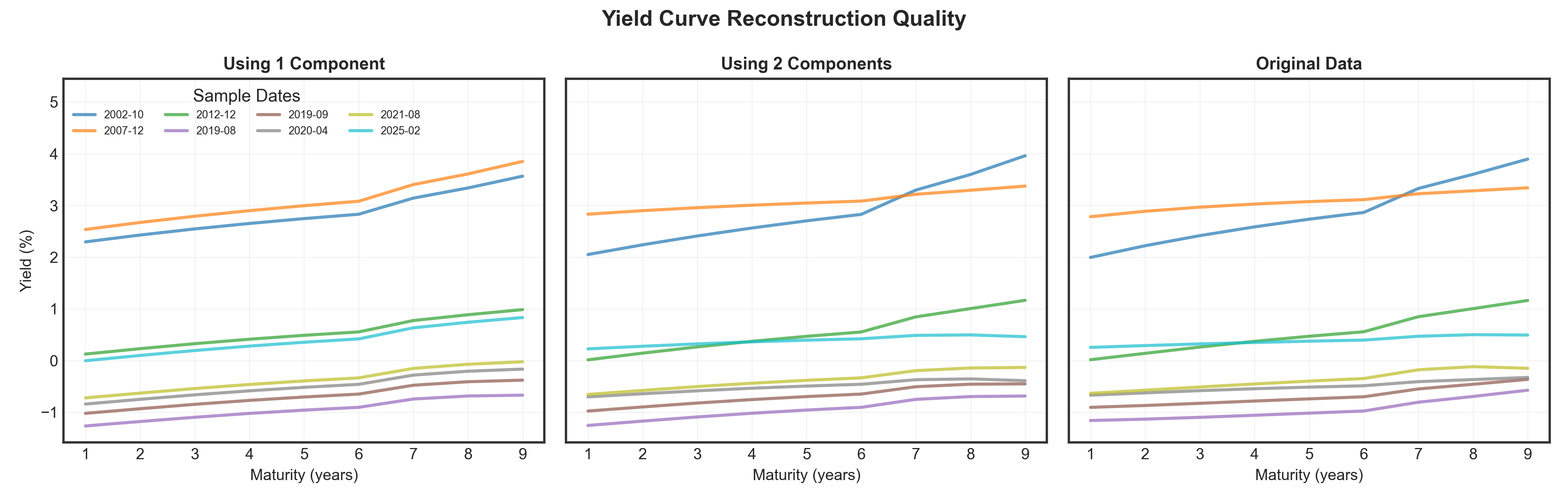
Transform & Reconstruct
Project the normalized data onto principal components, then reconstruct using only the top K components.
Show code
# Transform data to PC space
PC_scores = df_norm.dot(eigen_vectors)
# Select some random bond dates to track consistently
np.random.seed(1)
sample_indices = np.random.choice(len(df_norm), size=8, replace=False)
sample_indices = sorted(sample_indices)
# Use only the 9 yearly maturities that match our PCA dimensions
maturities = list(range(1, 10)) # 1Y through 9Y to match the 9 columns we used for PCA
# Create 3 panels: 1 Component, 2 Components, Original
fig, axes = plt.subplots(1, 3, figsize=(14, 4.5), sharey=True)
colors = plt.cm.tab10(np.linspace(0, 1, len(sample_indices)))
# Store all data for consistent y-axis scaling
all_data = []
# Panel 1: Reconstruction with 1 component
reconstructed_1 = PC_scores.iloc[:, :1].dot(eigen_vectors[:, :1].T)
reconstructed_1_denorm = reconstructed_1 * std.values + mean.values
all_data.extend(reconstructed_1_denorm.values.flatten())
for idx, sample_idx in enumerate(sample_indices):
date_label = df['date'].iloc[sample_idx]
axes[0].plot(maturities, reconstructed_1_denorm.iloc[sample_idx],
alpha=0.7, linewidth=2, color=colors[idx], label=date_label)
axes[0].set_title("Using 1 Component", fontsize=11, fontweight='bold')
axes[0].set_xlabel("Maturity (years)", fontsize=10)
axes[0].set_ylabel("Yield (%)", fontsize=10)
axes[0].grid(True, alpha=0.3)
# Panel 2: Reconstruction with 2 components
reconstructed_2 = PC_scores.iloc[:, :2].dot(eigen_vectors[:, :2].T)
reconstructed_2_denorm = reconstructed_2 * std.values + mean.values
all_data.extend(reconstructed_2_denorm.values.flatten())
for idx, sample_idx in enumerate(sample_indices):
axes[1].plot(maturities, reconstructed_2_denorm.iloc[sample_idx],
alpha=0.7, linewidth=2, color=colors[idx])
axes[1].set_title("Using 2 Components", fontsize=11, fontweight='bold')
axes[1].set_xlabel("Maturity (years)", fontsize=10)
axes[1].grid(True, alpha=0.3)
# Panel 3: Original data
for idx, sample_idx in enumerate(sample_indices):
original = df_yields.iloc[sample_idx].values
all_data.extend(original)
axes[2].plot(maturities, original,
alpha=0.7, linewidth=2, color=colors[idx])
axes[2].set_title("Original Data", fontsize=11, fontweight='bold')
axes[2].set_xlabel("Maturity (years)", fontsize=10)
axes[2].grid(True, alpha=0.3)
# Set consistent y-axis limits across all panels
y_min, y_max = min(all_data), max(all_data)
y_margin = (y_max - y_min) * 0.05
for ax in axes:
ax.set_ylim(y_min - y_margin, y_max + y_margin)
# Add overall title
fig.suptitle('Yield Curve Reconstruction Quality', fontsize=14, fontweight='bold', y=0.98)
# Add legend to the first panel only with 2 rows (horizontal layout)
axes[0].legend(title='Sample Dates', fontsize=7, loc='upper left', framealpha=0.9, ncol=4)
plt.tight_layout()
plt.show()Result
Just 3 numbers (PC1, PC2, PC3 scores) capture nearly all information in 13 yields! Notice how 1 component is too simple (flat), 2 components add slope, and 3 components capture full curve shapes.
🤔 Pop Quiz
If the first principal component of yield curves is “almost constant”, what does a positive PC1 value indicate?
- The yield curve is inverted (downward sloping)
- Short-term rates are higher than long-term rates
- Interest rates are higher across ALL maturities (parallel shift up)
- The curve has increased curvature
Case Study II: PCA Summary
Key Results
Dimensionality Reduction
- 9 correlated yields (13 in total) → 3 uncorrelated components
- 99.9% of variance retained
- Minimal information loss
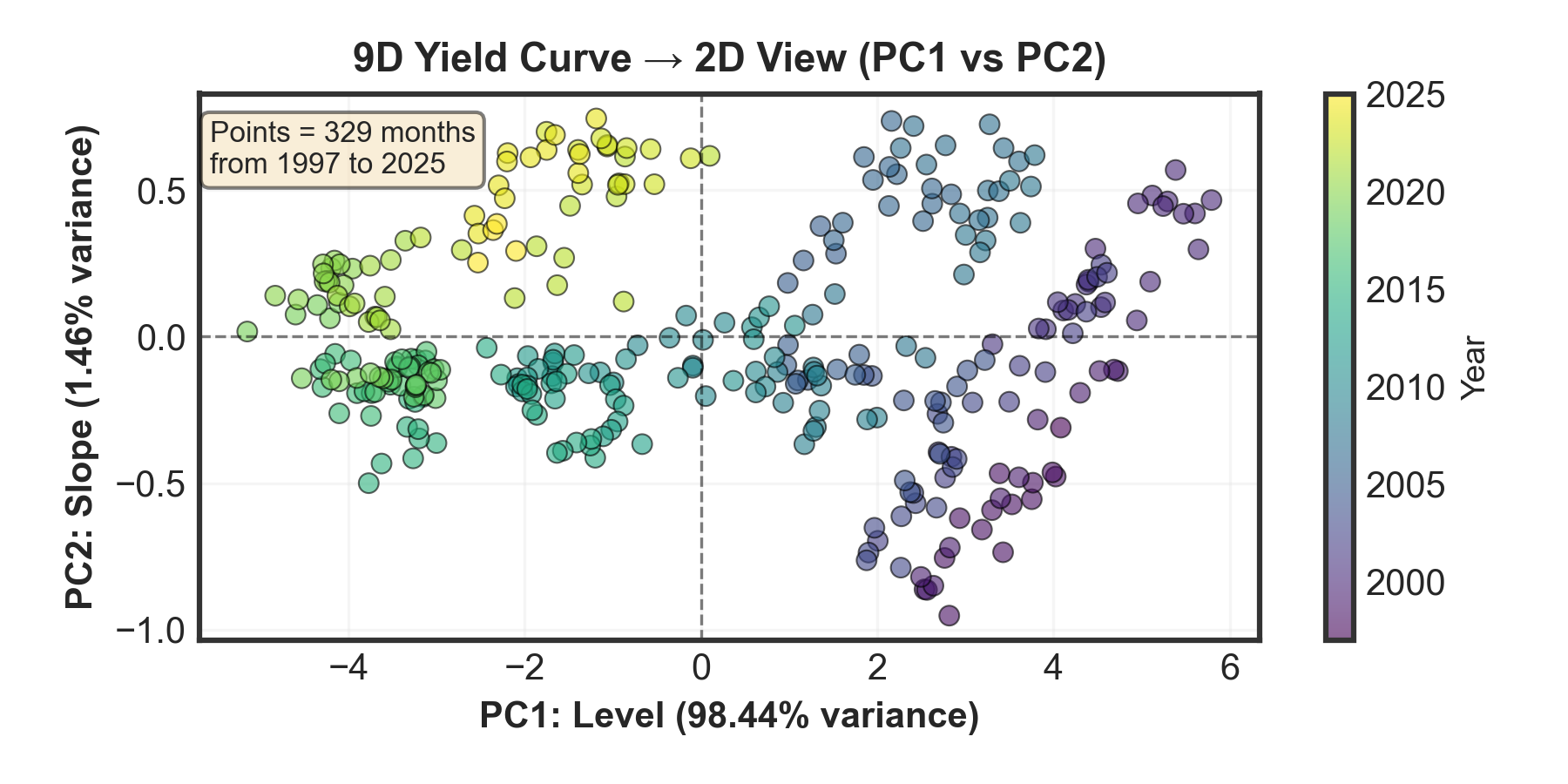
Three Components & 2D Plot Interpretation:
PC1 (Level): 98.44% variance — Parallel shift of entire curve
Horizontal axis: Movement left/right = interest rates rising/falling overallPC2 (Slope): 1.46% variance — Curve steepening/flattening
Vertical axis: Movement up/down = yield curve steepening/flatteningPC3 (Curvature): 0.09% variance — Mid-curve bending
Practical Value
When to use PCA:
- Many correlated variables
- Need dimensionality reduction
- Want to remove noise
- Linear relationships in data
Real applications:
- Interest rate modeling
- Portfolio risk analysis
- Customer segmentation
- Image compression
Important limitations:
- Only captures linear patterns
- Requires standardization
- Components are abstract
- Sensitive to outliers
From Cookbook to Your Project
Applying Today’s Lessons
You now have a complete workflow for your course project:
1. Acquire → Find/download your data (remember GIGO!)
2. Tidy → Check data types, missing values, duplicates
3. Explore (EDA) → Summary stats, distributions, scatter matrices
4. Visualize → Univariate plots → Multivariate plots → Group by categories
5. Transform (if needed) → Create derived variables, normalize, apply PCA
6. Communicate → Tell the story, highlight insights, recommend actions
Common Pitfalls to Avoid
| Pitfall | Why it’s bad | How to avoid |
|---|---|---|
| Skipping data checks | GIGO → wasted effort | Always run .info(), .describe(), check for NaNs |
| No univariate analysis | Miss obvious issues (outliers, errors) | Start with histograms/box plots BEFORE multivariate |
| Over-interpreting patterns | Correlation ≠ causation | Be cautious, seek domain expertise |
| Ignoring context | Statistical significance ≠ practical significance | Always ask: “What does this mean for the business?” |
| Poor communication | Great analysis, but no one understands it | Use clear visualizations, simple language, tell a story |
| Not iterating | First attempt is rarely the best | Revisit cleaning, feature engineering, visualization |
Remember: The first 80% of time is spent acquiring + wrangling data, not modeling!
Key Takeaways & Resources
Essential lessons:
Data Science is Iterative
- Acquire → Tidy → Explore → Visualize → Transform → Communicate (repeat!)
GIGO Principle
- Data quality determines project success (80% time on cleaning, 20% on modeling)
EDA Reveals Patterns
- Start univariate → multivariate → grouping to discover insights
PCA Simplifies Complexity
- Reduce 13 correlated variables → 2-3 key components (99% variance!)
Mortality Analysis
- For a good example of how to use entire data science pipeline, see Exercise Set 6 (HMD)
📚 Pipeline lecture | Project guidelines | Presentation tips
📅 Nov 12: Report | Nov 14: Slides | Nov 18: Presentations
Questions?
DSAS 2025 | HEC Lausanne