4 Modeling the spread of COVID-19 worldwide

In this section, we fit the logistic model to every country in the covid19_data_filtered dataset.

4.1 Fitting the logistic model to every country

Here we make use of the nested data, list-columns and logistic_model to fit the logistic model to every country in the dataset. Because, for some countries, the optimization method might not converge, we will use the possibly() function to see which ones fail and which ones succeed. Now one may wonder, for which country does the optimization fail ?

First, let’s fit the logistic model to every country and have a look at which one are not converging.

The countries for which the optimization fails are the following:

Denmark, Japan, Pakistan

We will also assess the goodness-of-fit of the logistic model in the various countries. Lets plot the residuals per country to have a look at the general trend of the residual in the model.

Comment: As we can see, the residuals seem to be quite close to zero, especially towards the end of the timeline (end of March, beginning of April), while at the beginning we can see some more distance from zero (given by the fact that the only country present in the dataset at that time is China, being the only one already in an epidemic situation). From the moment in which more countries join the dataset, we can see that the accuracy of the model increase, hence the residuals decrease and are closer to zero.

Let’s plot the residual per country to have a better look, and then we will zoom on the countries with the highest values of the residuals (meaning that they are the ones for which the model has a lower accuracy in the predictions).

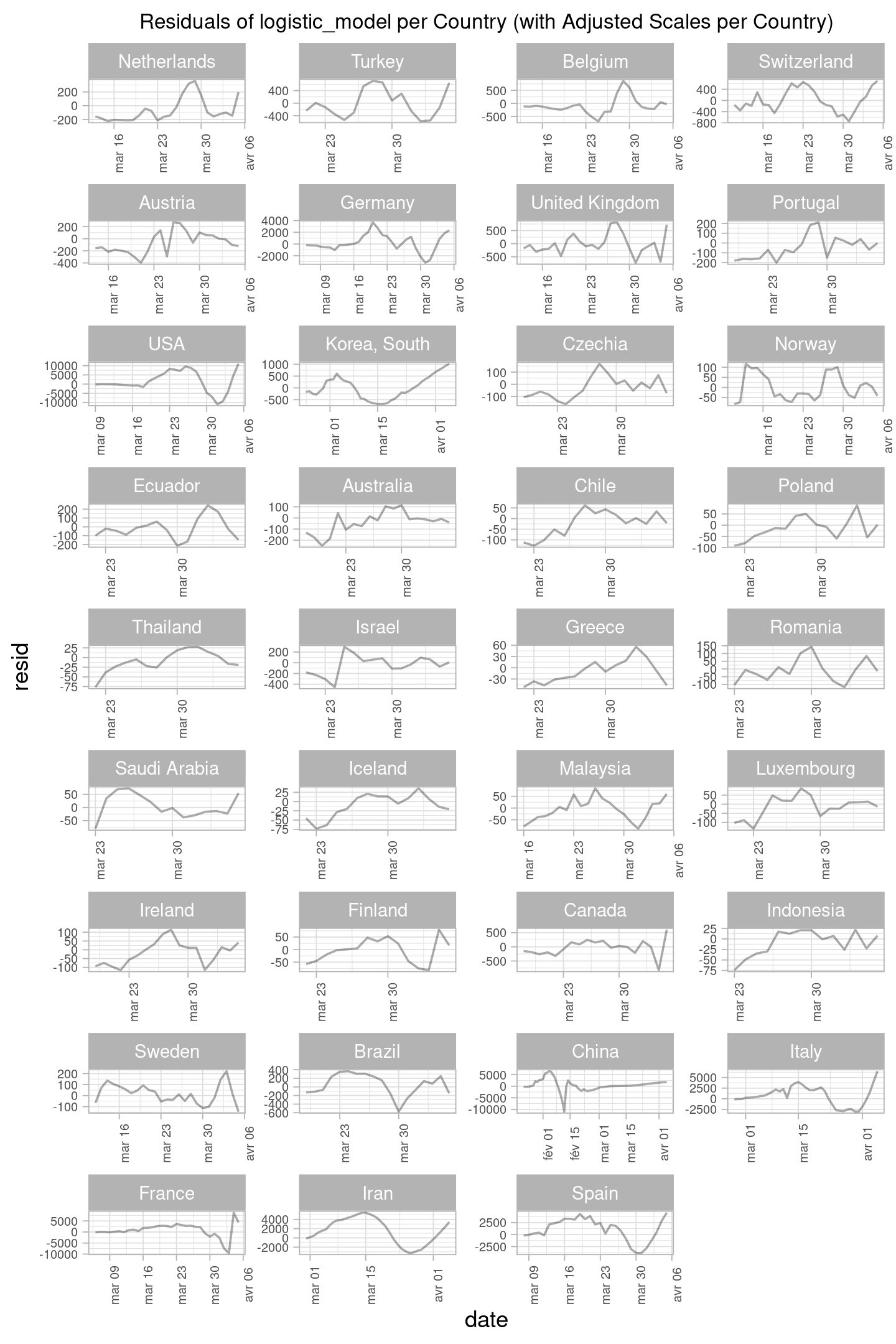Note: The axis are for this graph Residual of logistic_model per country and the one below has been adjusted for each country in order to be able to see better the different distributions.

Comment: As we can see the countries for which the model has the highest values for the residuals are China, France, Germany, Iran, Italy, South Korea, Spain and the USA. This does not come as a susprise, actually, since in the EDA part of our analysis, we have seen that they are the countries with the highest exponentiality in terms of absolute values of the confirmed cases (especially the US), while for China, as already mentioned, the residuals are higher at the beginning of the timeline, being the only country in the dataset, since we are considering only the countries in an epidemic situation.

We would like to also have also a score which shows the goodness-of-fit of the model for each country, however according to the (Burnham and Anderson 2002, 80), it is mentioned that AIC cannot be used for models with different number of observations (and also different datasets) as we see in the table below.

Number of observations per country
country	observations
Australia	19
Austria	23
Belgium	24
Brazil	18
Canada	19
Chile	15
China	75
Czechia	18
Ecuador	15
Finland	15
France	31
Germany	31
Greece	15
Iceland	15
Indonesia	14
Iran	37
Ireland	18
Israel	16
Italy	39
Korea, South	43
Luxembourg	16
Malaysia	21
Netherlands	24
Norway	26
Poland	15
Portugal	18
Romania	14
Saudi Arabia	14
Spain	29
Sweden	25
Switzerland	26
Thailand	15
Turkey	16
USA	28
United Kingdom	24

4.2 Fitted parameters and long-term predictions

We then describe the fitted parameters (i.e., the final size and the infection rates), both on a per-country basis and some aggregate numbers (e.g., total size of the epidemic over all considered countries). Furthermore, we study the evolution (say for \(t\) from 0 to 50) of the predictions of the number of confirmed cases from our models. Similarly as was discussed in the last sub-section of the exploratory data analysis, the number of confirmed cases per 100,000 habitants is also important to understand how specific countries are managing the spread of the epidemic. Thus, we predict the evolution of this number (i.e., by dividing our predictions for confirmed cases by the population size) and discuss.

We will do the aforementioned using the following functions:

• Format the fitted parameters using broom::tidy().
• For the long-term predictions, we use data = data.frame(t = 0:50) in add_predictions().

First we can see the parameters of the various models for each countries.

Fitted parameter per Country
country	K	R
Australia	6490	0.229
Austria	13475	0.227
Belgium	30106	0.192
Brazil	24528	0.194
Canada	26125	0.209
Chile	8226	0.178
China	80822	0.263
Czechia	7156	0.159
Ecuador	10116	0.131
Finland	4143	0.105
France	159261	0.185
Germany	114953	0.222
Greece	4636	0.093
Iceland	3258	0.094
Indonesia	4284	0.141
Iran	63936	0.175
Ireland	8411	0.167
Israel	10943	0.242
Italy	131962	0.201
Korea, South	9220	0.265
Luxembourg	3488	0.179
Malaysia	4802	0.148
Netherlands	24000	0.184
Norway	7300	0.143
Poland	16456	0.141
Portugal	15335	0.219
Romania	7725	0.180
Saudi Arabia	3811	0.159
Spain	141690	0.259
Sweden	26528	0.109
Switzerland	22253	0.227
Thailand	3162	0.151
Turkey	36048	0.311
United Kingdom	90683	0.201
USA	417895	0.280

Note: Please do note that we have rounded our results to 2 decimal places.

Comment: It doesn’t come as a surprise the fact that they vary quite a lot.

Now let’s look at the prediction per country.

Comment: We can see that the countries with the highest absolute values are the US, Spain, Germany, France and Italy (over a 100’000 of final confirmed cases predicted). This is in line with what we have found in the EDA part of our analysis.

In order to look at the aggregated sum, we can either use the logistic model on the filtered data and calculate new coefficients as we did with the swiss model but now applied to all countries and the second approach is to do it by region to use the fitted parameters of each country (nested) which makes more sense.

Comment: We can see that up to the 28th period the aggregated model predicts well however after that we do not have observations for most of the countries so it does not make sense to look at the observed values.

Note: Please do note that that the highest “t” belongs to China which is about 75 periods and therefore we have decided to extend our model to also include the all these dates. However, please do keep in mind that the 50th period the observation is mainly representative of predictions for China.

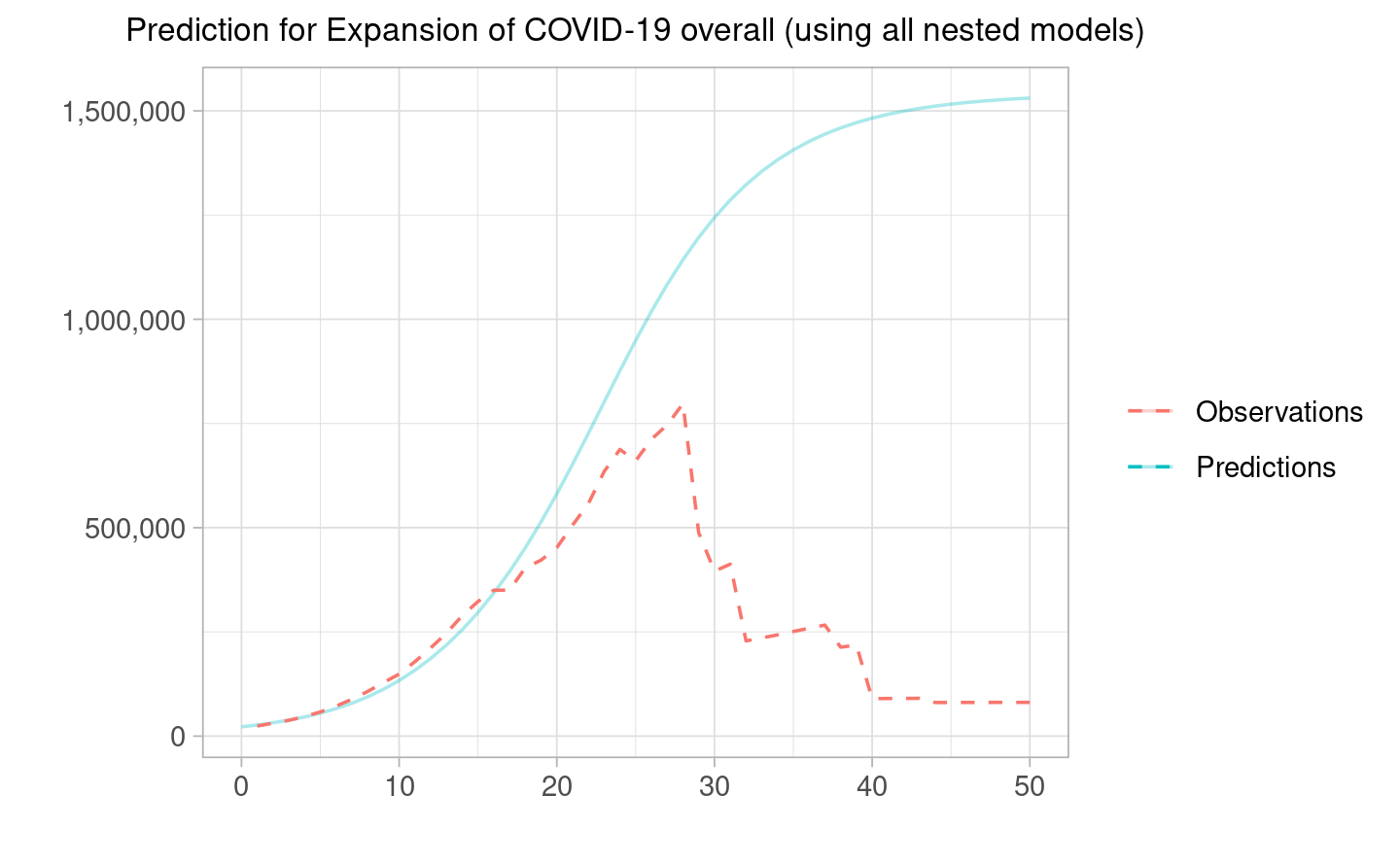
We can also do the aggregated sum for all countries only for the first 50 periods (because afterwards we do not have observed data points for almost all countries hence the observations naturally goes down). This model is a better one because it takes into account all the different coefficients rather than assigning the same one to all the countries.

Note: In the graph below, Please feel free to scroll over the country to see which one is contributing the most.

Comment: In terms of regions, we see the highest increase for North America due to the predicted increase for the US, followed by Europe & Central Asia, Italy, Spain and France among many and lastly, East Asian & Pacific with the most predicted cases for China.

Furthermore, referring back to the per-country predictions, we can also calculate the same for cases per 100,000 habitants displayed by the interactive plot below.

Comment: We can see that Iceland (green line) and Luxembourg (blue line) will have the highest number of confirmed cases per 100,000 habitants which is same as what we saw previously in the section of exploratory data analysis. This is due to their small populations and their infection numbers will be far larger than the countries that follow like Spain, Switzerland Belgium.

References

Burnham, Kenneth P., and David R. Anderson, eds. 2002. “Information and Likelihood Theory: A Basis for Model Selection and Inference.” In Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach, 49–97. New York, NY: Springer New York. https://doi.org/10.1007/978-0-387-22456-5_2.